顺序结构
顺序栈(Sequence Stack)
SqStack.cpp
/**
* @author huihut
* @E-mail:huihut@outlook.com
* @version 创建时间:2016年9月9日
* 说明:本程序实现了一个顺序栈。
* 功能:有初始化、销毁、判断空、清空、入栈、出栈、取元素的操作。
*/
#include "stdio.h"
#include "stdlib.h"
#include "malloc.h"
//5个常量定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -1
//测试程序长度定义
#define LONGTH 5
//类型定义
typedef int Status;
typedef int ElemType;
//顺序栈的类型
typedef struct {
ElemType *elem;
int top;
int size;
int increment;
} SqSrack;
//函数声明
Status InitStack_Sq(SqSrack &S, int size, int inc); //初始化顺序栈
Status DestroyStack_Sq(SqSrack &S); //销毁顺序栈
Status StackEmpty_Sq(SqSrack S); //判断S是否空,若空则返回TRUE,否则返回FALSE
void ClearStack_Sq(SqSrack &S); //清空栈S
Status Push_Sq(SqSrack &S, ElemType e); //元素e压入栈S
Status Pop_Sq(SqSrack &S, ElemType &e); //栈S的栈顶元素出栈,并用e返回
Status GetTop_Sq(SqSrack S, ElemType &e); //取栈S的栈顶元素,并用e返回
//初始化顺序栈
Status InitStack_Sq(SqSrack &S, int size, int inc) {
S.elem = (ElemType *)malloc(size * sizeof(ElemType));
if (NULL == S.elem) return OVERFLOW;
S.top = 0;
S.size = size;
S.increment = inc;
return OK;
}
//销毁顺序栈
Status DestroyStack_Sq(SqSrack &S) {
free(S.elem);
S.elem = NULL;
return OK;
}
//判断S是否空,若空则返回TRUE,否则返回FALSE
Status StackEmpty_Sq(SqSrack S) {
if (0 == S.top) return TRUE;
return FALSE;
}
//清空栈S
void ClearStack_Sq(SqSrack &S) {
if (0 == S.top) return;
S.size = 0;
S.top = 0;
}
//元素e压入栈S
Status Push_Sq(SqSrack &S, ElemType e) {
ElemType *newbase;
if (S.top >= S.size) {
newbase = (ElemType *)realloc(S.elem, (S.size + S.increment) * sizeof(ElemType));
if (NULL == newbase) return OVERFLOW;
S.elem = newbase;
S.size += S.increment;
}
S.elem[S.top++] = e;
return OK;
}
//取栈S的栈顶元素,并用e返回
Status GetTop_Sq(SqSrack S, ElemType &e) {
if (0 == S.top) return ERROR;
e = S.elem[S.top - 1];
return e;
}
//栈S的栈顶元素出栈,并用e返回
Status Pop_Sq(SqSrack &S, ElemType &e) {
if (0 == S.top) return ERROR;
e = S.elem[S.top - 1];
S.top--;
return e;
}
int main() {
//定义栈S
SqSrack S;
//定义测量值
int size, increment, i;
//初始化测试值
size = LONGTH;
increment = LONGTH;
ElemType e, eArray[LONGTH] = { 1, 2, 3, 4, 5 };
//显示测试值
printf("---【顺序栈】---\n");
printf("栈S的size为:%d\n栈S的increment为:%d\n", size, increment);
printf("待测试元素为:\n");
for (i = 0; i < LONGTH; i++) {
printf("%d\t", eArray[i]);
}
printf("\n");
//初始化顺序栈
if (!InitStack_Sq(S, size, increment)) {
printf("初始化顺序栈失败\n");
exit(0);
}
printf("已初始化顺序栈\n");
//入栈
for (i = 0; i < S.size; i++) {
if (!Push_Sq(S, eArray[i])) {
printf("%d入栈失败\n", eArray[i]);
exit(0);
}
}
printf("已入栈\n");
//判断非空
if(StackEmpty_Sq(S)) printf("S栈为空\n");
else printf("S栈非空\n");
//取栈S的栈顶元素
printf("栈S的栈顶元素为:\n");
printf("%d\n", GetTop_Sq(S, e));
//栈S元素出栈
printf("栈S元素出栈为:\n");
for (i = 0, e = 0; i < S.size; i++) {
printf("%d\t", Pop_Sq(S, e));
}
printf("\n");
//清空栈S
ClearStack_Sq(S);
printf("已清空栈S\n");
return 0;
}
顺序栈数据结构和图片
typedef struct {
ElemType *elem;
int top;
int size;
int increment;
} SqSrack;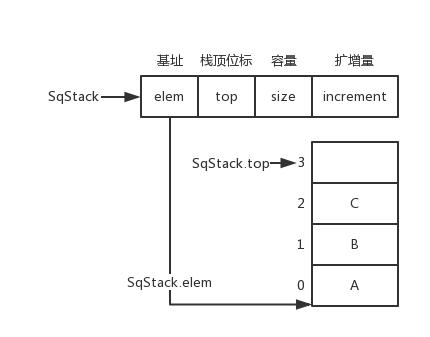
队列(Sequence Queue)
队列数据结构
typedef struct {
ElemType * elem;
int front;
int rear;
int maxSize;
}SqQueue;非循环队列
非循环队列图片
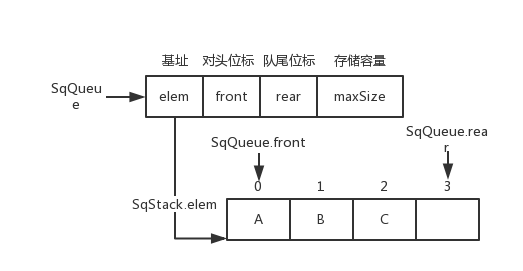
SqQueue.rear++
循环队列
循环队列图片
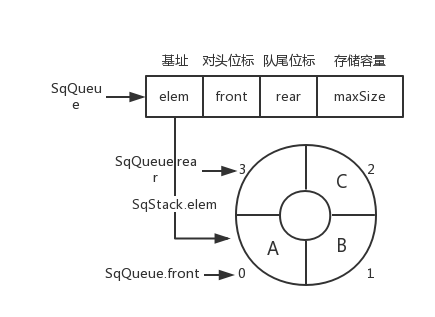
SqQueue.rear = (SqQueue.rear + 1) % SqQueue.maxSize
顺序表(Sequence List)
顺序表数据结构和图片
/**
* @author huihut
* @E-mail:huihut@outlook.com
* @version 创建时间:2016年9月9日
* 说明:本程序实现了一个顺序表。
*/
#include "stdio.h"
#include "stdlib.h"
#include "malloc.h"
//5个常量定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -1
//测试程序长度定义
#define LONGTH 5
//类型定义
typedef int Status;
typedef int ElemType;
//顺序栈的类型
typedef struct {
ElemType *elem;
int length;
int size;
int increment;
} SqList;
Status InitList_Sq(SqList &L, int size, int inc); //初始化顺序表L
Status DestroyList_Sq(SqList &L); //销毁顺序表L
Status ClearList_Sq(SqList &L); //将顺序表L清空
Status ListEmpty_Sq(SqList L); //若顺序表L为空表,则返回TRUE,否则FALSE
int ListLength_Sq(SqList L); //返回顺序表L中元素个数
Status GetElem_Sq(SqList L, int i, ElemType &e); //用e返回顺序表L中第i个元素的值
int Search_Sq(SqList L, ElemType e); //在顺序表L顺序查找元素e,成功时返回该元素在表中第一次出现的位置,否则返回-1
Status ListTraverse_Sq(SqList L, Status(*visit)(ElemType e)); //遍历顺序表L,依次对每个元素调用函数visit()
Status PutElem_Sq(SqList &L, int i, ElemType e); //将顺序表L中第i个元素赋值为e
Status Append_Sq(SqList &L, ElemType e); //在顺序表L表尾添加元素e
Status DeleteLast_Sq(SqList &L, ElemType &e); //删除顺序表L的表尾元素,并用参数e返回其值
//初始化顺序表L
Status InitList_Sq(SqList &L, int size, int inc) {
L.elem = (ElemType *)malloc(size * sizeof(ElemType));
if (NULL == L.elem) return OVERFLOW;
L.length = 0;
L.size = size;
L.increment = inc;
return OK;
}
//销毁顺序表L
Status DestroyList_Sq(SqList &L) {
free(L.elem);
L.elem = NULL;
return OK;
}
//将顺序表L清空
Status ClearList_Sq(SqList &L) {
if (0 != L.length) L.length = 0;
return OK;
}
//若顺序表L为空表,则返回TRUE,否则FALSE
Status ListEmpty_Sq(SqList L) {
if (0 == L.length) return TRUE;
return FALSE;
}
//返回顺序表L中元素个数
int ListLength_Sq(SqList L) {
return L.length;
}
// 用e返回顺序表L中第i个元素的值
Status GetElem_Sq(SqList L, int i, ElemType &e) {
e = L.elem[--i];
return OK;
}
// 在顺序表L顺序查找元素e,成功时返回该元素在表中第一次出现的位置,否则返回 - 1
int Search_Sq(SqList L, ElemType e) {
int i = 0;
while (i < L.length && L.elem[i] != e) i++;
if (i < L.length) return i;
else return -1;
}
//遍历调用
Status visit(ElemType e) {
printf("%d\t",e);
}
//遍历顺序表L,依次对每个元素调用函数visit()
Status ListTraverse_Sq(SqList L, Status(*visit)(ElemType e)) {
if (0 == L.length) return ERROR;
for (int i = 0; i < L.length; i++) {
visit(L.elem[i]);
}
return OK;
}
//将顺序表L中第i个元素赋值为e
Status PutElem_Sq(SqList &L, int i, ElemType e) {
if (i > L.length) return ERROR;
e = L.elem[--i];
return OK;
}
//在顺序表L表尾添加元素e
Status Append_Sq(SqList &L, ElemType e) {
if (L.length >= L.size) return ERROR;
L.elem[L.length] = e;
L.length++;
return OK;
}
//删除顺序表L的表尾元素,并用参数e返回其值
Status DeleteLast_Sq(SqList &L, ElemType &e) {
if (0 == L.length) return ERROR;
e = L.elem[L.length - 1];
L.length--;
return OK;
}
int main() {
//定义表L
SqList L;
//定义测量值
int size, increment, i;
//初始化测试值
size = LONGTH;
increment = LONGTH;
ElemType e, eArray[LONGTH] = { 1, 2, 3, 4, 5 };
//显示测试值
printf("---【顺序栈】---\n");
printf("表L的size为:%d\n表L的increment为:%d\n", size, increment);
printf("待测试元素为:\n");
for (i = 0; i < LONGTH; i++) {
printf("%d\t", eArray[i]);
}
printf("\n");
//初始化顺序表
if (!InitList_Sq(L, size, increment)) {
printf("初始化顺序表失败\n");
exit(0);
}
printf("已初始化顺序表\n");
//判空
if(TRUE == ListEmpty_Sq(L)) printf("此表为空表\n");
else printf("此表不是空表\n");
//入表
printf("将待测元素入表:\n");
for (i = 0; i < LONGTH; i++) {
if(ERROR == Append_Sq(L, eArray[i])) printf("入表失败\n");;
}
printf("入表成功\n");
//遍历顺序表L
printf("此时表内元素为:\n");
ListTraverse_Sq(L, visit);
//出表
printf("\n将表尾元素入表到e:\n");
if (ERROR == DeleteLast_Sq(L, e)) printf("出表失败\n");
printf("出表成功\n出表元素为%d\n",e);
//遍历顺序表L
printf("此时表内元素为:\n");
ListTraverse_Sq(L, visit);
//销毁顺序表
printf("\n销毁顺序表\n");
if(OK == DestroyList_Sq(L)) printf("销毁成功\n");
else printf("销毁失败\n");
return 0;
}顺序表数据结构和图片
typedef struct {
ElemType *elem;
int length;
int size;
int increment;
} SqList;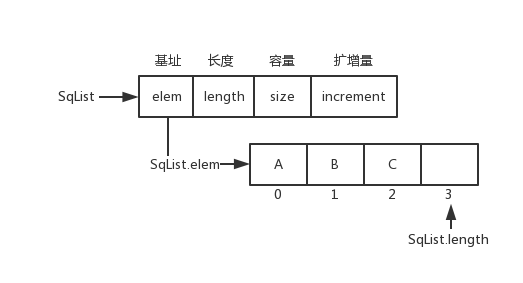
链式结构
LinkList.cpp
/**
* @author huihut
* @E-mail:huihut@outlook.com
* @version 创建时间:2016年9月18日
* 说明:本程序实现了一个单链表。
*/
#include "stdio.h"
#include "stdlib.h"
#include "malloc.h"
//5个常量定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -1
//类型定义
typedef int Status;
typedef int ElemType;
//测试程序长度定义
#define LONGTH 5
//链表的类型
typedef struct LNode {
ElemType data;
struct LNode *next;
} LNode, *LinkList;
Status InitList_L(LinkList &L);
Status DestroyList_L(LinkList &L);
Status ClearList_L(LinkList &L);
Status ListEmpty_L(LinkList L);
int ListLength_L(LinkList L);
LNode* Search_L(LinkList L, ElemType e);
LNode* NextElem_L(LNode *p);
Status InsertAfter_L(LNode *p, LNode *q);
Status DeleteAfter_L(LNode *p, ElemType &e);
void ListTraverse_L(LinkList L, Status(*visit)(ElemType e));
//创建包含n个元素的链表L,元素值存储在data数组中
Status create(LinkList &L, ElemType *data, int n) {
LNode *p, *q;
int i;
if (n < 0) return ERROR;
L = NULL;
p = L;
for (i = 0; i < n; i++)
{
q = (LNode *)malloc(sizeof(LNode));
if (NULL == q) return OVERFLOW;
q->data = data[i];
q->next = NULL;
if (NULL == p) L = q;
else p->next = q;
p = q;
}
return OK;
}
//e从链表末尾入链表
Status EnQueue_LQ(LinkList &L, ElemType &e) {
LinkList p, q;
if (NULL == (q = (LNode *)malloc(sizeof(LNode)))) return OVERFLOW;
q->data = e;
q->next = NULL;
if (NULL == L) L = q;
else
{
p = L;
while (p->next != NULL)
{
p = p->next;
}
p->next = q;
}
return OK;
}
//从链表头节点出链表到e
Status DeQueue_LQ(LinkList &L, ElemType &e) {
if (NULL == L) return ERROR;
LinkList p;
p = L;
e = p->data;
L = L->next;
free(p);
return OK;
}
//遍历调用
Status visit(ElemType e) {
printf("%d\t", e);
}
//遍历单链表
void ListTraverse_L(LinkList L, Status(*visit)(ElemType e))
{
if (NULL == L) return;
for (LinkList p = L; NULL != p; p = p -> next) {
visit(p -> data);
}
}
int main() {
int i;
ElemType e, data[LONGTH] = { 1, 2, 3, 4, 5 };
LinkList L;
//显示测试值
printf("---【单链表】---\n");
printf("待测试元素为:\n");
for (i = 0; i < LONGTH; i++) printf("%d\t", data[i]);
printf("\n");
//创建链表L
printf("创建链表L\n");
if (ERROR == create(L, data, LONGTH))
{
printf("创建链表L失败\n");
return -1;
}
printf("成功创建包含%d个元素的链表L\n元素值存储在data数组中\n", LONGTH);
//遍历单链表
printf("此时链表中元素为:\n");
ListTraverse_L(L, visit);
//从链表头节点出链表到e
printf("\n出链表到e\n");
DeQueue_LQ(L, e);
printf("出链表的元素为:%d\n", e);
printf("此时链表中元素为:\n");
//遍历单链表
ListTraverse_L(L, visit);
//e从链表末尾入链表
printf("\ne入链表\n");
EnQueue_LQ(L, e);
printf("入链表的元素为:%d\n", e);
printf("此时链表中元素为:\n");
//遍历单链表
ListTraverse_L(L, visit);
printf("\n");
return 0;
}
LinkList_with_head.cpp
/**
* @author huihut
* @E-mail:huihut@outlook.com
* @version 创建时间:2016年9月23日
* 说明:本程序实现了一个具有头结点的单链表。
*/
#include "stdio.h"
#include "stdlib.h"
#include "malloc.h"
//5个常量定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -1
//类型定义
typedef int Status;
typedef int ElemType;
//测试程序长度定义
#define LONGTH 5
//链表的类型
typedef struct LNode {
ElemType data;
struct LNode *next;
} LNode, *LinkList;
Status InitList_L(LinkList &L);
Status DestroyList_L(LinkList &L);
Status ClearList_L(LinkList &L);
Status ListEmpty_L(LinkList L);
int ListLength_L(LinkList L);
LNode* Search_L(LinkList L, ElemType e);
LNode* NextElem_L(LNode *p);
Status InsertAfter_L(LNode *p, LNode *q);
Status DeleteAfter_L(LNode *p, ElemType &e);
void ListTraverse_L(LinkList L, Status(*visit)(ElemType e));
//创建包含n个元素的链表L,元素值存储在data数组中
Status create(LinkList &L, ElemType *data, int n) {
LNode *p, *q;
int i;
if (n < 0) return ERROR;
p = L = NULL;
q = (LNode *)malloc(sizeof(LNode));
if (NULL == q) return OVERFLOW;
q->next = NULL;
p = L = q;
for (i = 0; i < n; i++)
{
q = (LNode *)malloc(sizeof(LNode));
if (NULL == q) return OVERFLOW;
q->data = data[i];
q->next = NULL;
p->next = q;
p = q;
}
return OK;
}
//e从链表末尾入链表
Status EnQueue_LQ(LinkList &L, ElemType &e) {
LinkList p, q;
if (NULL == (q = (LNode *)malloc(sizeof(LNode)))) return OVERFLOW;
q->data = e;
q->next = NULL;
if (NULL == L)
{
L = (LNode *)malloc(sizeof(LNode));
if (NULL == L) return OVERFLOW;
L -> next = q;
}
else if (NULL == L->next) L = q;
else
{
p = L;
while (p->next != NULL)
{
p = p->next;
}
p->next = q;
}
return OK;
}
//从链表头节点出链表到e
Status DeQueue_LQ(LinkList &L, ElemType &e) {
if (NULL == L || NULL == L->next) return ERROR;
LinkList p;
p = L->next;
e = p->data;
L->next = p->next;
free(p);
return OK;
}
//遍历调用
Status visit(ElemType e) {
printf("%d\t", e);
}
//遍历单链表
void ListTraverse_L(LinkList L, Status(*visit)(ElemType e))
{
if (NULL == L || NULL == L->next) return;
for (LinkList p = L -> next; NULL != p; p = p -> next) {
visit(p -> data);
}
}
int main() {
int i;
ElemType e, data[LONGTH] = { 1, 2, 3, 4, 5 };
LinkList L;
//显示测试值
printf("---【有头结点的单链表】---\n");
printf("待测试元素为:\n");
for (i = 0; i < LONGTH; i++) printf("%d\t", data[i]);
printf("\n");
//创建链表L
printf("创建链表L\n");
if (ERROR == create(L, data, LONGTH))
{
printf("创建链表L失败\n");
return -1;
}
printf("成功创建包含1个头结点、%d个元素的链表L\n元素值存储在data数组中\n", LONGTH);
//遍历单链表
printf("此时链表中元素为:\n");
ListTraverse_L(L, visit);
//从链表头节点出链表到e
printf("\n出链表到e\n");
DeQueue_LQ(L, e);
printf("出链表的元素为:%d\n", e);
printf("此时链表中元素为:\n");
//遍历单链表
ListTraverse_L(L, visit);
//e从链表末尾入链表
printf("\ne入链表\n");
EnQueue_LQ(L, e);
printf("入链表的元素为:%d\n", e);
printf("此时链表中元素为:\n");
//遍历单链表
ListTraverse_L(L, visit);
printf("\n");
return 0;
}链式数据结构
typedef struct LNode {
ElemType data;
struct LNode *next;
} LNode, *LinkList; 链队列(Link Queue)
链队列图片
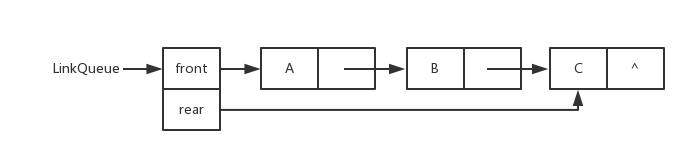
线性表的链式表示
单链表(Link List)
单链表图片
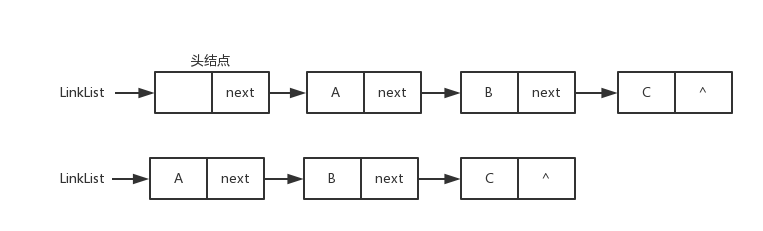
双向链表(Du-Link-List)
双向链表图片

循环链表(Cir-Link-List)
循环链表图片

哈希表
循环链表图片
#include<stdio.h>
#include<stdlib.h>
#define SUCCESS 1
#define UNSUCCESS 0
#define OVERFLOW -1
#define OK 1
#define ERROR -1
typedef int Status;
typedef int KeyType;
typedef struct{
KeyType key;
}RcdType;
typedef struct{
RcdType *rcd;
int size;
int count;
int *tag;
}HashTable;
int hashsize[] = { 11, 31, 61, 127, 251, 503 };
int index = 0;
Status InitHashTable(HashTable &H, int size){
int i;
H.rcd = (RcdType *)malloc(sizeof(RcdType)*size);
H.tag = (int *)malloc(sizeof(int)*size);
if (NULL == H.rcd || NULL == H.tag) return OVERFLOW;
for (i = 0; i< size; i++) H.tag[i] = 0;
H.size = size;
H.count = 0;
return OK;
}
int Hash(KeyType key, int m){
return (3 * key) % m;
}
void collision(int &p, int m){ //线性探测
p = (p + 1) % m;
}
Status SearchHash(HashTable H, KeyType key, int &p, int &c) {
p = Hash(key, H.size);
int h = p;
c = 0;
while ((1 == H.tag[p] && H.rcd[p].key != key) || -1 == H.tag[p]){
collision(p, H.size); c++;
}
if (1 == H.tag[p] && key == H.rcd[p].key) return SUCCESS;
else return UNSUCCESS;
}
void printHash(HashTable H) //打印哈希表
{
int i;
printf("key : ");
for (i = 0; i < H.size; i++)
printf("%3d ", H.rcd[i].key);
printf("\n");
printf("tag : ");
for (i = 0; i < H.size; i++)
printf("%3d ", H.tag[i]);
printf("\n\n");
}
Status InsertHash(HashTable &H, KeyType key); //对函数的声明
//重构
Status recreateHash(HashTable &H){
RcdType *orcd;
int *otag, osize, i;
orcd = H.rcd;
otag = H.tag;
osize = H.size;
InitHashTable(H, hashsize[index++]);
//把所有元素,按照新哈希函数放到新表中
for (i = 0; i < osize; i++){
if (1 == otag[i]){
InsertHash(H, orcd[i].key);
}
}
}
Status InsertHash(HashTable &H, KeyType key){
int p, c;
if (UNSUCCESS == SearchHash(H, key, p, c)){ //没有相同key
if (c*1.0 / H.size < 0.5){ //冲突次数未达到上线
//插入代码
H.rcd[p].key = key;
H.tag[p] = 1;
H.count++;
return SUCCESS;
}
else recreateHash(H); //重构哈希表
}
return UNSUCCESS;
}
Status DeleteHash(HashTable &H, KeyType key){
int p, c;
if (SUCCESS == SearchHash(H, key, p, c)){
//删除代码
H.tag[p] = -1;
H.count--;
return SUCCESS;
}
else return UNSUCCESS;
}
void main()
{
printf("-----哈希表-----\n");
HashTable H;
int i;
int size = 11;
KeyType array[8] = { 22, 41, 53, 46, 30, 13, 12, 67 };
KeyType key;
RcdType e;
//初始化哈希表
printf("初始化哈希表\n");
if (SUCCESS == InitHashTable(H, hashsize[index++])) printf("初始化成功\n");
//插入哈希表
printf("插入哈希表\n");
for (i = 0; i <= 7; i++){
key = array[i];
InsertHash(H, key);
printHash(H);
}
//删除哈希表
printf("删除哈希表\n");
int p, c;
if (SUCCESS == DeleteHash(H, 12)) {
printf("删除成功,此时哈希表为:\n");
printHash(H);
}
//查询哈希表
printf("查询哈希表\n");
if (SUCCESS == SearchHash(H, 67, p, c)) printf("查询成功\n");
//再次插入,测试哈希表的重构
printf("再次插入,测试哈希表的重构:\n");
KeyType array1[8] = { 27, 47, 57, 47, 37, 17, 93, 67 };
for (i = 0; i <= 7; i++){
key = array1[i];
InsertHash(H, key);
printHash(H);
}
}链地址法实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define HASHSIZE 10
typedef unsigned int uint;
typedef struct Node
{
const char *key;
const char *value;
Node *next;
} Node;
class HashTable
{
private:
Node *node[HASHSIZE];
public:
HashTable();
uint hash(const char *key);
Node *lookup(const char *key);
bool install(const char *key, const char *value);
const char *get(const char *key);
void display();
};
HashTable::HashTable()
{
for (int i = 0; i < HASHSIZE; ++i)
{
node[i] = NULL;
}
}
uint HashTable::hash(const char *key)
{
uint hash = 0;
for (; *key; ++key)
{
hash = hash * 33 + *key;
}
return hash % HASHSIZE;
}
Node *HashTable::lookup(const char *key)
{
Node *np;
uint index;
index = hash(key);
for (np = node[index]; np; np = np->next)
{
if (!strcmp(key, np->key))
return np;
}
return NULL;
}
bool HashTable::install(const char *key, const char *value)
{
uint index;
Node *np;
if (!(np = lookup(key)))
{
index = hash(key);
np = (Node *)malloc(sizeof(Node));
if (!np)
return false;
np->key = key;
np->next = node[index];
node[index] = np;
}
np->value = value;
return true;
}
void HashTable::display()
{
Node *temp;
for (int i = 0; i < HASHSIZE; ++i)
{
if (!node[i])
{
printf("[]\n");
}
else
{
printf("[");
for (temp = node[i]; temp; temp = temp->next)
{
printf("[%s][%s] ", temp->key, temp->value);
}
printf("]\n");
}
}
}
const char *HashTable::get(const char *key)
{
Node *node = this->lookup(key);
return node ? node->value : nullptr;
}
int main(int argc, char const *argv[])
{
HashTable *ht = new HashTable();
const char *key[] = {"a", "b", "c"};
const char *value[] = {"value1", "value2", "fuck"};
for (int i = 0; i < 3; ++i)
{
ht->install(key[i], value[i]);
}
ht->display();
return 0;
}概念
哈希函数:H(key): K -> D , key ∈ K
构造方法
- 直接定址法
- 除留余数法
- 数字分析法
- 折叠法
- 平方取中法
冲突处理方法
- 链地址法:key 相同的用单链表链接
- 开放定址法
- 线性探测法:key 相同 -> 放到 key 的下一个位置,
Hi = (H(key) + i) % m - 二次探测法:key 相同 -> 放到
Di = 1^2, -1^2, ..., ±(k)^2,(k<=m/2) - 随机探测法:
H = (H(key) + 伪随机数) % m
- 线性探测法:key 相同 -> 放到 key 的下一个位置,
线性探测的哈希表数据结构
线性探测的哈希表数据结构和图片
typedef char KeyType;
typedef struct {
KeyType key;
}RcdType;
typedef struct {
RcdType *rcd;
int size;
int count;
bool *tag;
}HashTable;
递归
概念
函数直接或间接地调用自身
递归与分治
- 分治法
- 问题的分解
- 问题规模的分解
- 折半查找(递归)
- 归并查找(递归)
- 快速排序(递归)
递归与迭代
- 迭代:反复利用变量旧值推出新值
- 折半查找(迭代)
- 归并查找(迭代)
广义表
头尾链表存储表示
广义表的头尾链表存储表示和图片
// 广义表的头尾链表存储表示
typedef enum {ATOM, LIST} ElemTag;
// ATOM==0:原子,LIST==1:子表
typedef struct GLNode {
ElemTag tag;
// 公共部分,用于区分原子结点和表结点
union {
// 原子结点和表结点的联合部分
AtomType atom;
// atom 是原子结点的值域,AtomType 由用户定义
struct {
struct GLNode *hp, *tp;
} ptr;
// ptr 是表结点的指针域,prt.hp 和 ptr.tp 分别指向表头和表尾
} a;
} *GList, GLNode;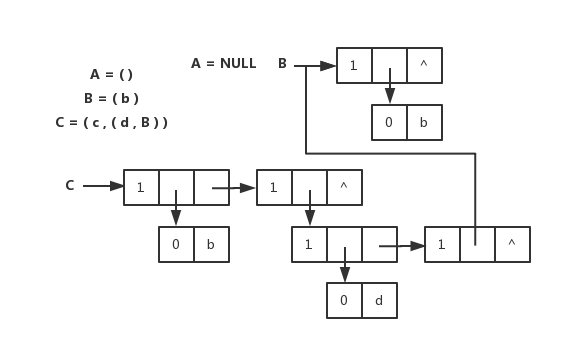
扩展线性链表存储表示
扩展线性链表存储表示和图片
// 广义表的扩展线性链表存储表示
typedef enum {ATOM, LIST} ElemTag;
// ATOM==0:原子,LIST==1:子表
typedef struct GLNode1 {
ElemTag tag;
// 公共部分,用于区分原子结点和表结点
union {
// 原子结点和表结点的联合部分
AtomType atom; // 原子结点的值域
struct GLNode1 *hp; // 表结点的表头指针
} a;
struct GLNode1 *tp;
// 相当于线性链表的 next,指向下一个元素结点
} *GList1, GLNode1;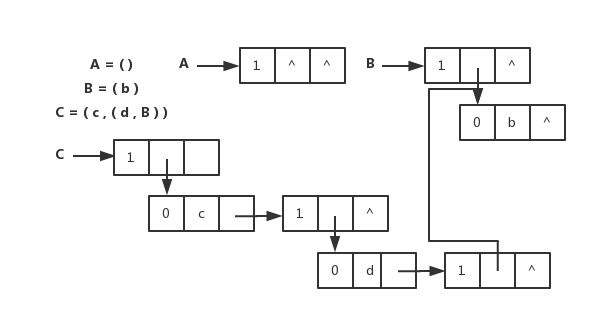
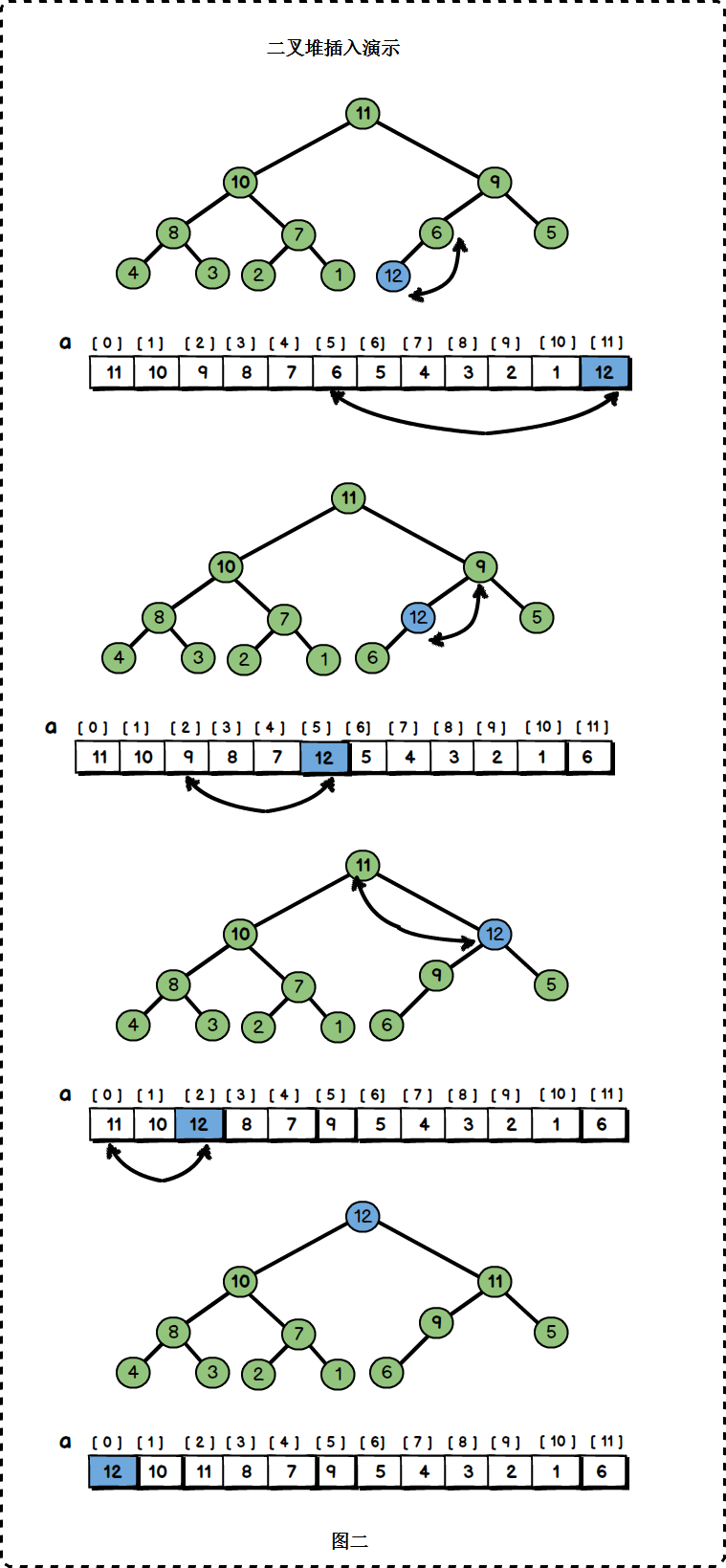
二叉堆
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
template <class T>
class MinHeap
{
public:
MinHeap()
{
}
MinHeap(const vector<T> &array)
{
for (const auto &e : array)
{
Insert(e);
}
}
void Insert(const T &x)
{
m_array.push_back(x); //将数据插入到最后
AdjustUp(m_array.size() - 1); //从最后一个数组往上调整堆,使之还是一个二叉堆
}
bool RemoveHeapTop()
{
//检查堆中是否还有元素
if (m_array.size() == 0)
{
return false;
}
//将最后一个结点的值给第一个结点,并删除最后一个结点
m_array[0] = m_array[m_array.size() - 1];
m_array.pop_back();
AdjustDown(0); //重新往下做调整
return true;
}
// 堆顶元素
T Top()
{
return m_array[0];
}
// 打印元素
void Print()
{
for (const auto &el : m_array)
{
cout << el << " ";
}
cout << endl;
}
// 用stl里面的方法验证他是不是小顶堆
bool IsHeap()
{
return is_heap(m_array.begin(), m_array.end(), greater<>());
}
// 堆小顶堆升序排列
void Sort()
{
int size = m_array.size();
vector<T> array;
while (size--)
{
array.push_back(m_array[0]); // 肯定是最小的
RemoveHeapTop(); // 移除第一个元素,调整之后还让他是小顶堆
}
m_array.swap(array);
}
private:
void AdjustDown(int root)
{
T value = m_array[root]; //保存当前结点的值
int size = m_array.size();
int left = root * 2 + 1; //当前结点的左孩子
while (left < size)
{
// 找出左右结点中的最小值
int right = left + 1; //当前结点的右孩子
int min = (right < size && m_array[left] > m_array[right]) ? right : left;
if (value > m_array[min])
{
m_array[root] = m_array[min];
root = min;
left = root * 2 + 1;
}
else
{
break;
}
}
m_array[root] = value;
}
void AdjustUp(int child)
{
T value = m_array[child]; //插入节点的值
//一直向上调整直到根结点的值小于左右结点
while (child > 0)
{
int root = (child - 1) / 2; // 父节点所以
if (value < m_array[root])
{
m_array[child] = m_array[root];
child = root;
}
else
{
break;
}
}
m_array[child] = value; //需要被调整的值插入到最后的正确位置
}
vector<T> m_array;
};
int main()
{
MinHeap<int> minHeap(vector<int>{80, 40, 30, 60, 90, 70, 10, 50, 20});
cout << minHeap.IsHeap() << endl;
minHeap.Insert(31);
cout << minHeap.IsHeap() << endl;
minHeap.RemoveHeapTop();
cout << minHeap.IsHeap() << endl;
minHeap.Print();
minHeap.Sort();
minHeap.Print();
return 0;
}
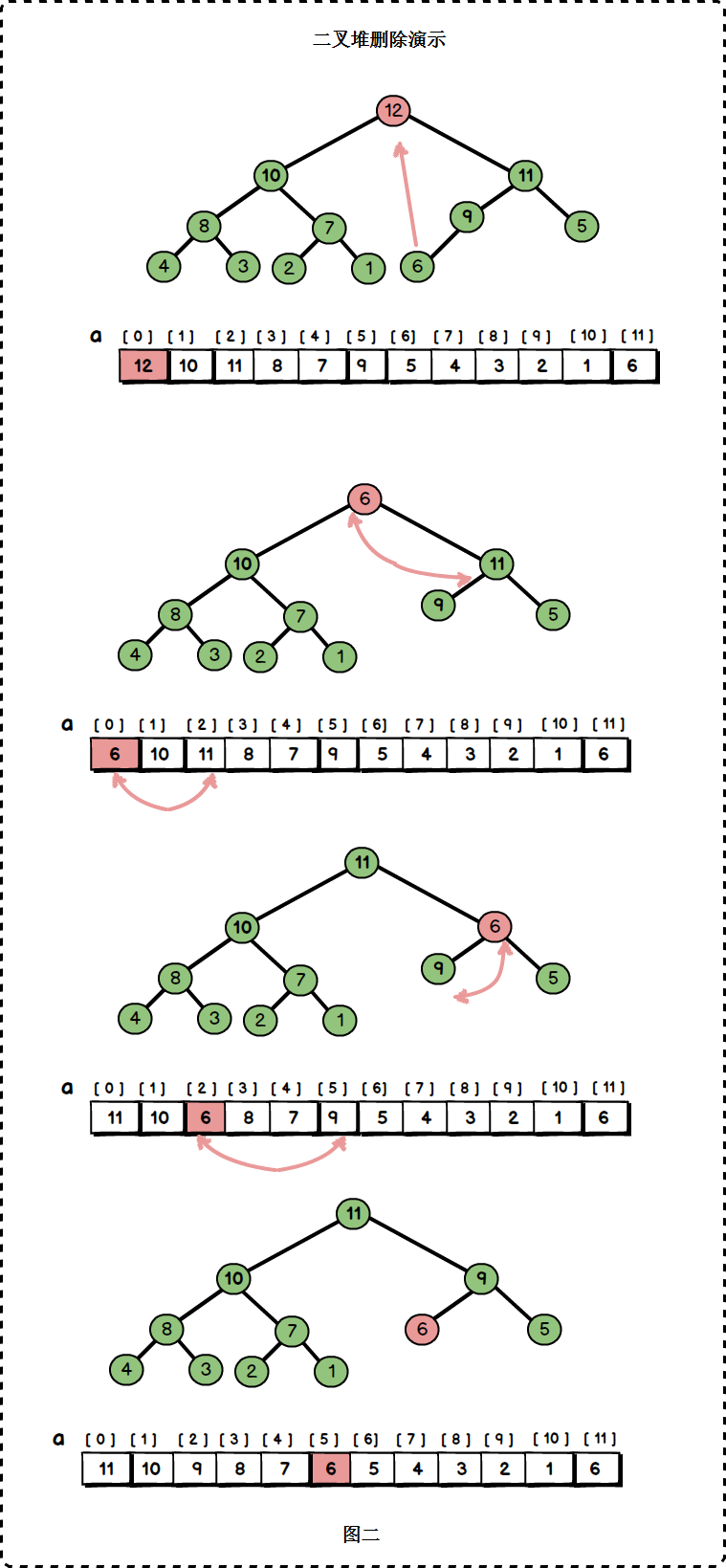
二叉树
BinaryTree.cpp
#include<stdio.h>
#include<stdlib.h>
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -1
#define SUCCESS 1
#define UNSUCCESS 0
#define dataNum 5
int i = 0;
int dep = 0;
char data[dataNum] = { 'A', 'B', 'C', 'D', 'E' };
typedef int Status;
typedef char TElemType;
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
void InitBiTree(BiTree &T); //创建一颗空二叉树
BiTree MakeBiTree(TElemType e, BiTree L, BiTree R); //创建一颗二叉树T,其中根节点的值为e,L和R分别作为左子树和右子树
void DestroyBiTree(BiTree &T); //销毁二叉树
Status BiTreeEmpty(BiTree T); //对二叉树判空。若为空返回TRUE,否则FALSE
Status BreakBiTree(BiTree &T, BiTree &L, BiTree &R); //将一颗二叉树T分解成根、左子树、右子树三部分
Status ReplaceLeft(BiTree &T, BiTree <); //替换左子树。若T非空,则用LT替换T的左子树,并用LT返回T的原有左子树
Status ReplaceRight(BiTree &T, BiTree &RT); //替换右子树。若T非空,则用RT替换T的右子树,并用RT返回T的原有右子树
int Leaves(BiTree T);
int Depth(BiTree T);
Status visit(TElemType e);
void UnionBiTree(BiTree &Ttemp);
//InitBiTree空二叉树是只有一个BiTree指针?还是有一个结点但结点域为空?
void InitBiTree(BiTree &T)
{
T = NULL;
}
BiTree MakeBiTree(TElemType e, BiTree L, BiTree R)
{
BiTree t;
t = (BiTree)malloc(sizeof(BiTNode));
if (NULL == t) return NULL;
t->data = e;
t->lchild = L;
t->rchild = R;
return t;
}
Status visit(TElemType e)
{
printf("%c", e);
return OK;
}
int Leaves(BiTree T) //对二叉树T求叶子结点数目
{
int l = 0, r = 0;
if (NULL == T) return 0;
if (NULL == T->lchild && NULL == T->rchild) return 1;
//问题分解,2个子问题
//求左子树叶子数目
l = Leaves(T->lchild);
//求右子树叶子数目
r = Leaves(T->rchild);
//组合
return r + l;
}
int depTraverse(BiTree T) //层次遍历:dep是个全局变量,高度
{
if (NULL == T) return ERROR;
dep = (depTraverse(T->lchild) > depTraverse(T->rchild)) ? depTraverse(T->lchild) : depTraverse(T->rchild);
return dep + 1;
}
void levTraverse(BiTree T, Status(*visit)(TElemType e), int lev) //高度遍历:lev是局部变量,层次
{
if (NULL == T) return;
visit(T->data);
printf("的层次是%d\n", lev);
levTraverse(T->lchild, visit, ++lev);
levTraverse(T->rchild, visit, lev);
}
void InOrderTraverse(BiTree T, Status(*visit)(TElemType e), int &num) //num是个全局变量
{
if (NULL == T) return;
visit(T->data);
if (NULL == T->lchild && NULL == T->rchild) { printf("是叶子结点"); num++; }
else printf("不是叶子结点");
printf("\n");
InOrderTraverse(T->lchild, visit, num);
InOrderTraverse(T->rchild, visit, num);
}
Status BiTreeEmpty(BiTree T)
{
if (NULL == T) return TRUE;
return FALSE;
}
Status BreakBiTree(BiTree &T, BiTree &L, BiTree &R)
{
if (NULL == T) return ERROR;
L = T->lchild;
R = T->rchild;
T->lchild = NULL;
T->rchild = NULL;
return OK;
}
Status ReplaceLeft(BiTree &T, BiTree <)
{
BiTree temp;
if (NULL == T) return ERROR;
temp = T->lchild;
T->lchild = LT;
LT = temp;
return OK;
}
Status ReplaceRight(BiTree &T, BiTree &RT)
{
BiTree temp;
if (NULL == T) return ERROR;
temp = T->rchild;
T->rchild = RT;
RT = temp;
return OK;
}
void UnionBiTree(BiTree &Ttemp)
{
BiTree L = NULL, R = NULL;
L = MakeBiTree(data[i++], NULL, NULL);
R = MakeBiTree(data[i++], NULL, NULL);
ReplaceLeft(Ttemp, L);
ReplaceRight(Ttemp, R);
}
int main()
{
BiTree T = NULL, Ttemp = NULL;
InitBiTree(T);
if (TRUE == BiTreeEmpty(T)) printf("初始化T为空\n");
else printf("初始化T不为空\n");
T = MakeBiTree(data[i++], NULL, NULL);
Ttemp = T;
UnionBiTree(Ttemp);
Ttemp = T->lchild;
UnionBiTree(Ttemp);
Status(*visit1)(TElemType);
visit1 = visit;
int num = 0;
InOrderTraverse(T, visit1, num);
printf("叶子结点是 %d\n", num);
printf("叶子结点是 %d\n", Leaves(T));
int lev = 1;
levTraverse(T, visit1, lev);
printf("高度是 %d\n", depTraverse(T));
return 0;
}性质
- 非空二叉树第 i 层最多 2(i-1) 个结点 (i >= 1)
- 深度为 k 的二叉树最多 2k - 1 个结点 (k >= 1)
- 度为 0 的结点数为 n0,度为 2 的结点数为 n2,则 n0 = n2 + 1
- 有 n 个结点的完全二叉树深度 k = ⌊ log2(n) ⌋ + 1
- 对于含 n 个结点的完全二叉树中编号为 i (1 <= i <= n) 的结点
- 若 i = 1,为根,否则双亲为 ⌊ i / 2 ⌋
- 若 2i > n,则 i 结点没有左孩子,否则孩子编号为 2i
- 若 2i + 1 > n,则 i 结点没有右孩子,否则孩子编号为 2i + 1
存储结构
二叉树数据结构
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;顺序存储
二叉树顺序存储图片
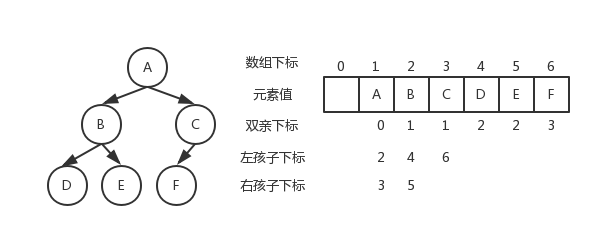
链式存储
二叉树链式存储图片

遍历方式
| 遍历方法 | 顺序 | 示意图 | 应用 |
|---|---|---|---|
| 前序 | 根 ➜ 左 ➜ 右 | 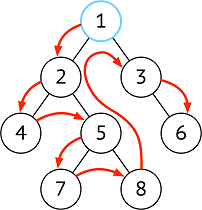 |
想在节点上直接执行操作(或输出结果)使用先序 |
| 中序 | 左 ➜ 根 ➜ 右 | 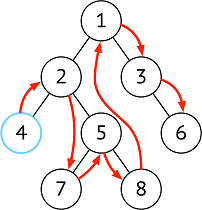 |
在二分搜索树中,中序遍历的顺序符合从小到大(或从大到小)顺序的要输出排序好的结果使用中序 |
| 后序 | 左 ➜ 右 ➜ 根 |  |
后续遍历的特点是在执行操作时,肯定已经遍历过该节点的左右子节点适用于进行破坏性操作比如删除所有节点,比如判断树中是否存在相同子树 |
| 广度优先 | 层序,横向访问 |  |
当树的高度非常高(非常瘦)使用广度优先剑节省空间 |
| 深度优先 | 纵向,探底到叶子节点 | 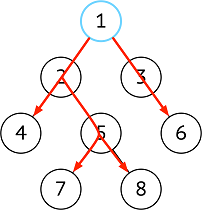 |
当每个节点的子节点非常多(非常胖),使用深度优先遍历节省空间(访问顺序和入栈顺序相关,想当于先序遍历) |
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
// 节点结构体
struct Node
{
int value;
Node *left;
Node *right;
Node(int value) : value(value), left(NULL), right(NULL) {}
};
// 前序遍历递归实现
void preOrder(Node *node)
{
if (node)
{
cout << node->value << " ";
preOrder(node->left);
preOrder(node->right);
}
}
// 前序遍历非递归实现(也是深度优先搜索)
void preOrder1(Node *node)
{
if (node == NULL)
{
return;
}
stack<Node *> nstack;
nstack.push(node);
while (!nstack.empty())
{
Node *temp = nstack.top();
cout << temp->value << " ";
nstack.pop();
if (temp->right)
{
nstack.push(temp->right);
}
if (temp->left)
{
nstack.push(temp->left);
}
}
}
// 中序遍历递归实现
void inOrder(Node *node)
{
if (node)
{
inOrder(node->left);
cout << node->value << " ";
inOrder(node->right);
}
}
// 中序遍历非递归实现
void inOrder1(Node *node)
{
stack<Node *> nstack;
Node *temp = node;
while (temp || !nstack.empty())
{
if (temp)
{
nstack.push(temp);
temp = temp->left;
}
else
{
temp = nstack.top();
cout << temp->value << " ";
nstack.pop();
temp = temp->right;
}
}
}
// 后序遍历递归实现
void posOrder(Node *node)
{
if (node)
{
posOrder(node->left);
posOrder(node->right);
cout << node->value << " ";
}
}
// 后序遍历非递归实现
void posOrder1(Node *node)
{
if (node == NULL)
return;
stack<Node *> nstack1, nstack2;
nstack1.push(node);
while (!nstack1.empty())
{
Node *temp = nstack1.top();
nstack1.pop();
nstack2.push(temp);
if (temp->left)
nstack1.push(temp->left);
if (temp->right)
nstack1.push(temp->right);
}
while (!nstack2.empty())
{
cout << nstack2.top()->value << " ";
nstack2.pop();
}
}
// 广度优先遍历
void broadOrder(Node *node)
{
if (!node)
{
return;
}
queue<Node *> qnodes;
qnodes.push(node);
while (!qnodes.empty())
{
Node *temp = qnodes.front();
cout << temp->value << " ";
qnodes.pop();
if (temp->left)
{
qnodes.push(temp->left);
}
if (temp->right)
{
qnodes.push(temp->right);
}
}
}
int main()
{
vector<Node> nodes;
nodes.emplace_back(Node(0)); // 存粹是为了值跟索引一致好初始化加的一个节点
// 按照图片初始化二叉树
int value = 0;
while (value++ <= 8)
{
Node node(value);
nodes.emplace_back(node);
}
nodes[1].left = &nodes[2];
nodes[1].right = &nodes[3];
nodes[2].left = &nodes[4];
nodes[2].right = &nodes[5];
nodes[3].right = &nodes[6];
nodes[5].left = &nodes[7];
nodes[5].right = &nodes[8];
Node root = nodes[1];
cout << "preOrder is:";
preOrder(&root);
cout << endl;
cout << "inOrder is:";
inOrder(&root);
cout << endl;
cout << "PosOrder is:";
posOrder(&root);
cout << endl;
cout << "PreOrder without recursion is:";
preOrder1(&root);
cout << endl;
cout << "inOrder without recursion is:";
inOrder1(&root);
cout << endl;
cout << "PosOrder without recursion is:";
posOrder1(&root);
cout << endl;
cout << "BroadOrder is:";
broadOrder(&root);
cout << endl;
}
//preOrder is : 1 2 4 5 7 8 3 6
//inOrder is : 4 2 7 5 8 1 3 6
//PosOrder is : 4 7 8 5 2 6 3 1
//PreOrder without recursion is : 1 2 4 5 7 8 3 6
//inOrder without recursion is : 4 2 7 5 8 1 3 6
//PosOrder without recursion is : 4 7 8 5 2 6 3 1
//BroadOrder is : 1 2 3 4 5 6 7 8分类
- 满二叉树
- 完全二叉树(堆)
- 大顶堆:根 >= 左 && 根 >= 右
- 小顶堆:根 <= 左 && 根 <= 右
- 二叉查找树(二叉排序树):左 < 根 < 右
- 平衡二叉树(AVL树):| 左子树树高 - 右子树树高 | <= 1
- 最小失衡树:平衡二叉树插入新结点导致失衡的子树:调整:
- LL型:根的左孩子右旋
- RR型:根的右孩子左旋
- LR型:根的左孩子左旋,再右旋
- RL型:右孩子的左子树,先右旋,再左旋
其他树及森林
树的存储结构
- 双亲表示法
- 双亲孩子表示法
- 孩子兄弟表示法
并查集
一种不相交的子集所构成的集合 S = {S1, S2, ..., Sn}
平衡二叉树(AVL树)
性质
- | 左子树树高 - 右子树树高 | <= 1
- 平衡二叉树必定是二叉搜索树,反之则不一定
- 最小二叉平衡树的节点的公式:
F(n)=F(n-1)+F(n-2)+1(1 是根节点,F(n-1) 是左子树的节点数量,F(n-2) 是右子树的节点数量)
平衡二叉树图片

最小失衡树
平衡二叉树插入新结点导致失衡的子树
调整:
- LL 型:根的左孩子右旋
- RR 型:根的右孩子左旋
- LR 型:根的左孩子左旋,再右旋
- RL 型:右孩子的左子树,先右旋,再左旋
红黑树
红黑树的特征是什么?
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是 NIL 节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)(新增节点的父节点必须相同)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。(新增节点必须为红)
调整
- 变色
- 左旋
- 右旋
应用
- 关联数组:如 STL 中的 map、set
红黑树、B 树、B+ 树的区别?
- 红黑树的深度比较大,而 B 树和 B+ 树的深度则相对要小一些
- B+ 树则将数据都保存在叶子节点,同时通过链表的形式将他们连接在一起。
B 树(B-tree)、B+ 树(B+-tree)
B 树、B+ 树图片
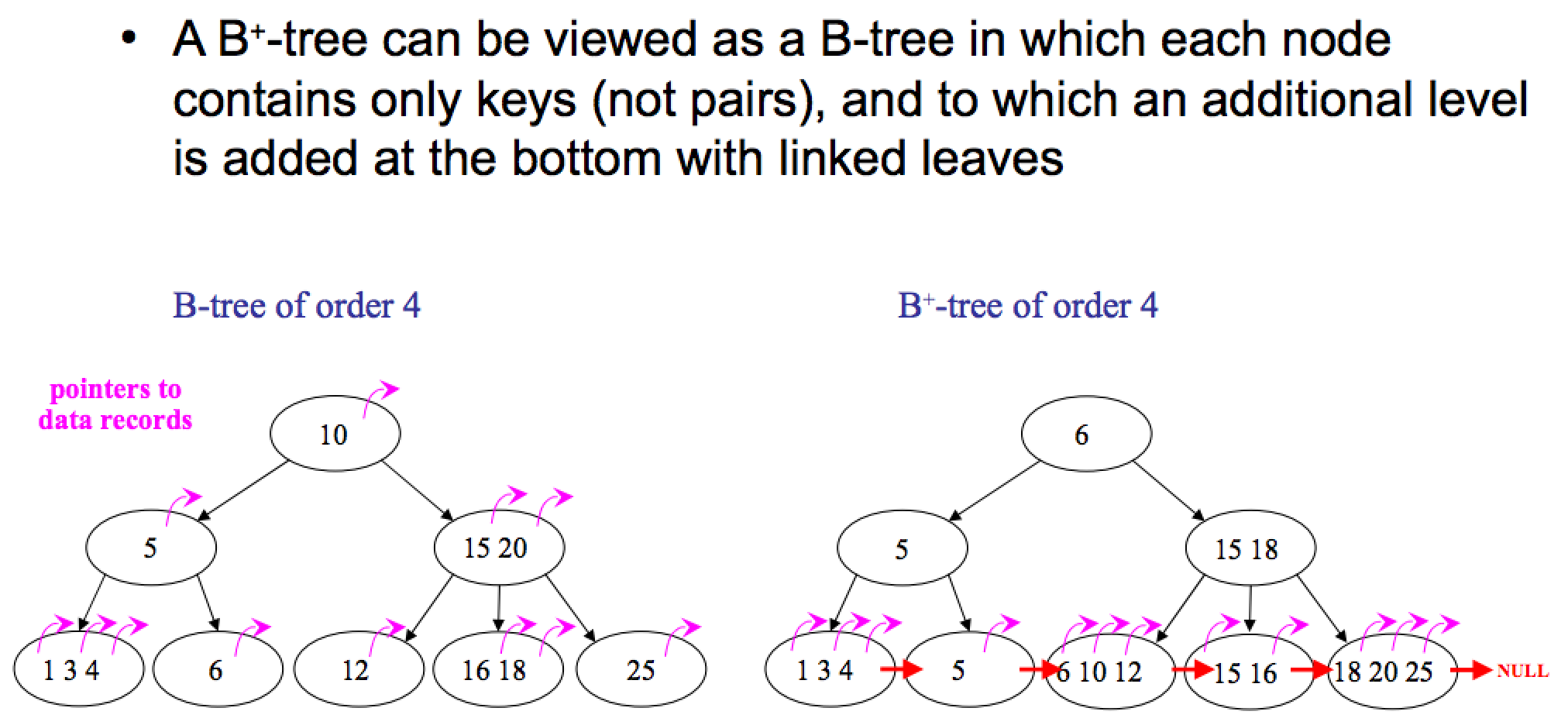
特点
- 一般化的二叉查找树(binary search tree)
- “矮胖”,内部(非叶子)节点可以拥有可变数量的子节点(数量范围预先定义好)
应用
- 大部分文件系统、数据库系统都采用B树、B+树作为索引结构
区别
- B+树中只有叶子节点会带有指向记录的指针(ROWID),而B树则所有节点都带有,在内部节点出现的索引项不会再出现在叶子节点中。
- B+树中所有叶子节点都是通过指针连接在一起,而B树不会。
B树的优点
对于在内部节点的数据,可直接得到,不必根据叶子节点来定位。
B+树的优点
- 非叶子节点不会带上 ROWID,这样,一个块中可以容纳更多的索引项,一是可以降低树的高度。二是一个内部节点可以定位更多的叶子节点。
- 叶子节点之间通过指针来连接,范围扫描将十分简单,而对于B树来说,则需要在叶子节点和内部节点不停的往返移动。
B 树、B+ 树区别来自:differences-between-b-trees-and-b-trees、B树和B+树的区别
八叉树
八叉树图片
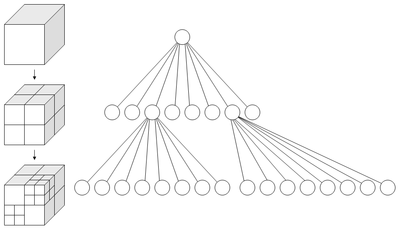
八叉树(octree),或称八元树,是一种用于描述三维空间(划分空间)的树状数据结构。八叉树的每个节点表示一个正方体的体积元素,每个节点有八个子节点,这八个子节点所表示的体积元素加在一起就等于父节点的体积。一般中心点作为节点的分叉中心。
用途
- 三维计算机图形
- 最邻近搜索
例题
单向链表反转
// 递归方式:实现单链表反转
ListNode *ReverseList(ListNode *head)
{
// 递归终止条件:找到链表最后一个结点
if (head == nullptr || head->next == nullptr)
return head;
else
{
ListNode *newhead = ReverseList(head->next); // 先反转后面的链表,从最后面的两个结点开始反转,依次向前
head->next->next = head; // 将后一个链表结点指向前一个结点
head->next = nullptr; // 将原链表中前一个结点指向后一个结点的指向关系断开
return newhead;
}
}
//非递归方式:实现单链表反转
ListNode *reverseList(ListNode *head)
{
if (head == nullptr || head->next == nullptr)
return head;
ListNode *prev = head;
ListNode *cur = head->next;
ListNode *temp = nullptr;
while (cur)
{
temp = cur->next; // temp作为中间节点,记录当前结点的下一个节点的位置
cur->next = prev; // 当前结点指向前一个节点
prev = cur; // 指针后移
cur = temp; // 指针后移,处理下一个节点
}
head->next = nullptr; // while结束后,将翻转后的最后一个节点(即翻转前的第一个结点head)的链域置为nullptr
return prev;
}链表中环的入口节点
ListNode *MeetingNode(ListNode *pHead)
{
if (pHead == nullptr)
return nullptr;
ListNode *pSlow = pHead->m_pNext;
if (pSlow == nullptr)
return nullptr;
ListNode *pFast = pSlow->m_pNext;
while (pFast != nullptr && pSlow != nullptr)
{
if (pFast == pSlow)
return pFast;
pSlow = pSlow->m_pNext;
pFast = pFast->m_pNext;
if (pFast != nullptr)
pFast = pFast->m_pNext;
}
return nullptr;
}
ListNode *EntryNodeOfLoop(ListNode *pHead)
{
ListNode *meetingNode = MeetingNode(pHead);
if (meetingNode == nullptr)
return nullptr;
// 得到环中结点的数目
int nodesInLoop = 1;
ListNode *pNode1 = meetingNode;
while (pNode1->m_pNext != meetingNode)
{
pNode1 = pNode1->m_pNext;
++nodesInLoop;
}
// 先移动pNode1,次数为环中结点的数目
pNode1 = pHead;
for (int i = 0; i < nodesInLoop; ++i)
pNode1 = pNode1->m_pNext;
// 再移动pNode1和pNode2
ListNode *pNode2 = pHead;
while (pNode1 != pNode2)
{
pNode1 = pNode1->m_pNext;
pNode2 = pNode2->m_pNext;
}
return pNode1;
}如何判断两个链表是否相交并求出相交点
合并两个排序的链表
ListNode *Merge(ListNode *pHead1, ListNode *pHead2)
{
if (pHead1 == nullptr)
return pHead2;
else if (pHead2 == nullptr)
return pHead1;
ListNode *pMergedHead = nullptr;
if (pHead1->m_nValue < pHead2->m_nValue)
{
pMergedHead = pHead1;
pMergedHead->m_pNext = Merge(pHead1->m_pNext, pHead2);
}
else
{
pMergedHead = pHead2;
pMergedHead->m_pNext = Merge(pHead1, pHead2->m_pNext);
}
return pMergedHead;
}跳表
找出数组中出现次数超过一半的数
- 用快速排序,处于中间的数就是要找的那个数
- 使用Map统计每个数的个数
-
抵消法
int FindMostData(int arr[], int len) { int findNum = 0; // 出现次数超过一半的数; int count = 0; // 只要最终count > 0,那么对应的findNum就是出现次数超过一半的数; // 循环过程中,i每增加一次,就相当于把i之前的所有元素 //(除了满足“findNum == arr[i]”条件的arr[i],这些对应元素用“count++”来标记)都抛弃了, // 但是之后每当执行一次“ count-- ”时,又会从前面这些已保留的且等于findNum的元素中删除一项,直到count == 0,再重选findNum; for (int i = 0; i < len; i++) { if (count == 0) // count为0时,表示当前的findNum需要重选; { findNum = arr[i]; count = 1; } else { count += (findNum == arr[i]); } } return findNum; }
1000个苹果分10个箱装
1000个苹果放入10个箱子。客户如果要获得1~1000个苹果中的任意个数,都可以整箱搬,而不用拆开箱子。问是否有这样的装箱方法?
二进制数组合:1,10,100,1000 。可以表示任何0X01~0XFF之间的数字。
判断一个数是否是2的幂次方
将2的幂次方写成二进制形式后,很容易就会发现有一个特点:二进制中只有一个1,并且1后面跟了n个0
// 判断是不是2的幂次方
bool is2Pow(int number)
{
return (number & number - 1) == 0;
}
// 递归判断一个数是2的多少次方
int log2(int value)
{
if (value == 1)
return 0;
else
return 1 + log2(value >> 1);
}Top-K
- 简单粗暴排序
- 每次剔除一个最大的元素,直至第k个
- 用最小堆实现
- 基于快速排序划分思想的二分法
100亿个数字排序
问题:给100亿个数字排序,但是内存只有4G。磁盘空间无限大。
分析:100亿个 int 型数字放在文件里面大概有 10000000000 * 4 / 1024 / 1024 / 1024 = 37.3GB,非常大,4G 的内存一次装不下了。那么肯定是要拆分成小的文件一个一个来处理,最终在合并成一个排好序的大文件。
思路:先将文件拆开,比如100个,这样每份文件37.3GB / 100 = 373Mb的内存就可以排序好。100个小文件内部排好序之后,就要把这些内部有序的小文件,合并成一个大的文件,可以用二叉堆来做100路合并的操作,每个小文件是一路,合并后的大文件仍然有序。具体流程如下:
- 首先遍历100个文件,每个文件里面取第一个数字,组成 (数字, 文件号) 这样的组合加入到堆里(假设是从小到大排序,用小顶堆),遍历完后堆里有100个 (数字,文件号)这样的元素
- 然后不断从堆顶拿元素出来,每拿出一个元素,把它的文件号读取出来,然后去对应的文件里,加一个元素进入堆,直到那个文件被读取完。拿出来的元素当然追加到最终结果的文件里。
- 按照上面的操作,直到堆被取空了,此时最终结果文件里的全部数字就是有序的了。
typedef struct node // 队列结点
{
int data;
int id; // 文件的编号
bool operator<(const node &a) const
{
return data < a.data;
}
} node;
// 将 100 个有序文件合并成一个文件, K 路归并排序
int sort()
{
std::priority_queue<node> q; // 优先队列的结构,在优先队列中,优先级高的元素先出队列
node tmp, p;
// 打开需要最终排序好的文件
FILE *out = fopen(result, "wt");
FILE *file[FILE_NUM];
for (int i = 0; i < FILE_NUM; i++)
{
// 打开全部哈希文件
char hashfile[512];
sprintf(hashfile, "%s\\hash_%d.~tmp", tmpdir, i);
file[i] = fopen(hashfile, "rt");
// 从每个文件取第一个数(因为是排序过的,所以肯定是最大或最小)初始化堆
fscanf(file[i], "%d", &tmp.data);
tmp.id = i;
q.push(tmp);
}
// 开始 K 路归并,即不断的从已排序过的文件中拿数字放到堆中
// 然后从堆中将堆顶的数字写入最终文件中
while (!q.empty())
{
// 将堆顶的元素写回磁盘,
tmp = q.top();
q.pop();
fprintf(out, "%d\n", tmp.data);
// 再从当前的已排序过的文件中拿一个放到堆中
if (fscanf(file[tmp.id], "%d", &p.data) != EOF)
{
p.id = tmp.id;
q.push(p);
}
}
return 1;
}连续子数组最大和
给定一个数组 array[1, 4, -5, 9, 8, 3, -6],在这个数字中有多个子数组,子数组和最大的应该是:[9, 8, 3],输出20,再比如数组为[1, -2, 3, 10, -4, 7, 2, -5],和最大的子数组为[3, 10, -4, 7, 2],输出18。
// 动态规划(DP) 不难得出,针对这个问题,递推公式是DP[i] = max{DP[i-1] + A[i],A[i]};
// 既然转移方程出来了,意味着写一层循环就可以解决这个问题。
int maxSum(const vector<int> &vec)
{
int maxsum = INT_MIN, sum = 0;
for(int i = 0; i < vec.size(); i++)
{
sum = max(sum + vec[i], vec[i]);
maxsum = max(maxsum, sum);
}
return maxsum;
}
// 暴力求解
int maxSum(const vector<int> &vec)
{
int maxsum = INT_MIN, sum = 0;
for(int i = 0; i < vec.size(); i++)
{
int cursum = 0;
for(int j = i; j < vec.size(); j++)
{
cursum += vec[j];
maxsum = max(maxsum, cursum);
}
}
return maxsum;
}